Linear methods are my favourite for elegance. I’m not sure any other area of applied maths has such a rich toolbox of practical theorems to draw from. A basic application of linear methods are linear regression models. However, in a machine learning setting, the have some problems, including: (1) that they typically have few degrees of freedom and therefore saturate quickly, and (2) that they imply a rigid geometry (a hyper-plane) which is often unrealistic.
We can alleviate both problems. It turns out that we can express similarity between data points as a Gram matrix and then do linear regression directly to it, otherwise known as “kernel” regression. The proverbial \(Ax \approx b\) becomes \(Kx \approx b\) where \(K\) is a \(m \times m\) Gram matrix (given \(m\) data points). Suddenly we have as many parameters as there are data points (addressing the saturation problem), so more usually we would fit a regularised version like \((K^\top K + I\lambda)x \approx K^\top b\) instead.
The radial basis kernel (RBF), \(K(x,x') = exp (-\gamma || x-x' || ^2)\), is a similarity measure based on an exponentially tapering squared Euclidean distance: \(\gamma\) decides how quickly it tapers. If we form the matrix \(K\) by calculating \(K(x,x')\) for every pair of data points, we can fit the model in the usual way: \(\alpha = (K^\top K + I\lambda)^+ K^\top b\). The prediction function is given by \(y_i = \alpha \cdot K(x_i, \cdot)\): note that the contribution of each component is weighted by (exponentially tapering) similarity to all other data points, which changes the geometry of the model dependent on its locality, thereby addressing the rigid geometry problem.
An issue with Kernel methods is that the space complexity is quadratic due to the \(m \times m\) Kernel matrix. One way to scale kernels to much bigger data is through kernel approximation by basis expansion. For the RBF kernel, an extremely elegant such method is known as “random Fourier features”. It was introduced in a seminal paper which went on to win the NIPS 2017 test of time award.
The RBF kernel basis vectors are created by randomly sampling the Fourier transform of the kernel:
\[\phi(x) = \sqrt{\frac{2}{D}} \bigg[cos(g_1(x)),sin(g_1(x)), ..., cos(g_D(x)),sin(g_D(x))\bigg]\]
where \(g_i(x) = \omega_i^\top x+b_i\), and \(\omega_i, b_i\) are sampled \(D\) times, such that \(\omega_i \sim N(0,\gamma^{-1})\) and \(b_i \sim [0,2\pi]\). Note that the space complexity of the approximation is \(O(mD)\), so we are able to apply it to much bigger than data.
Let’s give it a go in R. Here is some Boston housing data:
require(mlbench, quietly=T)
data("BostonHousing")
X <- BostonHousing[, -which(names(BostonHousing)=="medv")]
X$chas <- as.numeric(as.character(X$chas))
X <- as.matrix(X)
y <- matrix(BostonHousing$medv, ncol=1)Here is the correlation between the response and a linear regression:
const <- matrix(rep(1,NROW(X)), ncol=1)
X_ <- cbind(const, X)
beta <- solve(t(X_) %*% X_) %*% t(X_) %*% y
y_ <- X_ %*% beta
lr_cor = cor(y,y_)
lr_cor## [,1]
## [1,] 0.860606Here is a routine to generate Fourier random features, fit them and test the correlation.
go <- function(D=200, gam=1, lam=0.1) {
W <- matrix(rnorm(D * NCOL(X), mean=0, sd=1/gam),
nrow=D)
B <- runif(D, min=0, max=2*pi)
X_ <- sweep(X %*% t(W), 2, B, "+")
X_ <- cbind(cos(X_), sin(X_)) / sqrt(2/D)
const <- matrix(rep(1,NROW(X)), ncol=1)
X_ <- cbind(const, X_)
I <- diag(ncol(X_))
beta <- solve(t(X_) %*% X_ + lam * I) %*% t(X_) %*% y
y_ <- X_ %*% beta
cor(y,y_)
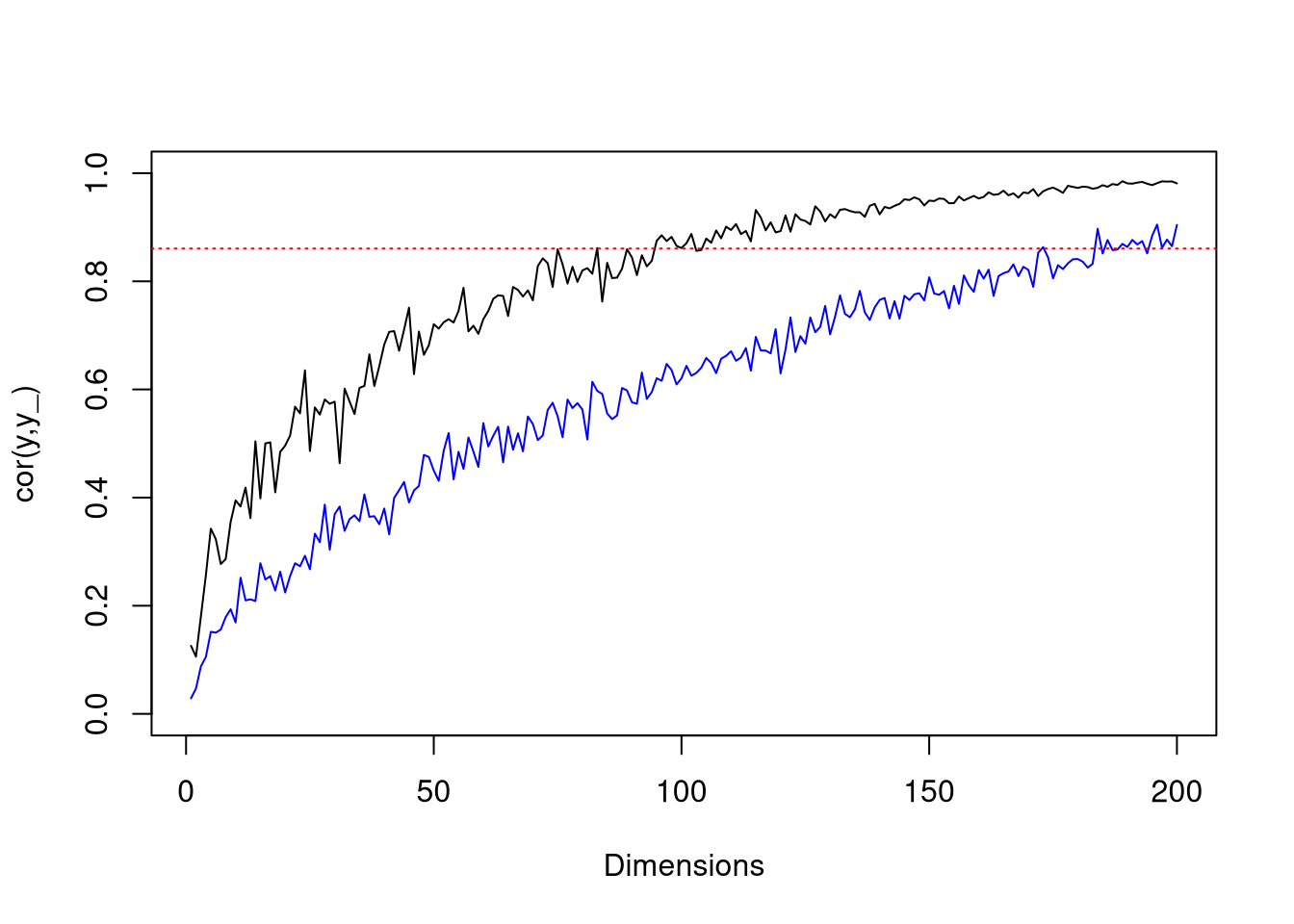
}Here are some plots to illustrate the effect of dimension on correlation, and and gamma on convergence ($ and \(\gamma=1\) for black and blue lines respectively). The dotted red line is the correlation achieved with linear regression.
plot (
sapply(1:200, \(i) go(i,gam=12)),
pch=19, cex=0.25, ylim=c(0,1), type="l",
xlab="Dimensions", ylab="cor(y,y_)")
lines (
sapply(1:200, \(i) go(i, gam=1)),
pch=19, cex=0.25, col="blue")
abline(h=lr_cor, lty="dotted", col="red")