INTRODUCTION
[If you want to have a go straight away, jump to the examples at the bottom of this post.]
Making a novel logic puzzle has been a bucket list item for me since yesteryear and I was finally handy enough with Prolog to endeavour for something elegant without having to write reams of code. I arbitrarily decided that I wanted the puzzle to be expressed in terms of Dominoe tiles. I tried a whole bunch of ideas which either resulted in eventual nonsense or puzzles which were too easy to solve. Eventually, I came up with “Domicles”; a fun and challenging puzzle, presented herein with examples and a Prolog implementation.
DOMICLES
“Domicles” is a combinatorial game using standard (double-6) Dominoe tiles. It is most enjoyable when played with a physical set of tiles. Here is an easy game:

The tiles are arranged 4x2 making a grid of 4x4 numbers as above. The aim of the game is to swap the tiles around such that every row and column in the 4x4 number grid has only unique values. The tiles cannot be flipped or rotated; just moved to different locations in the 4x2 layout.
Let’s solve the first example. The puzzle above has duplicates in grid columns 2 and 4, and grid row 2. Clearly 4|0 and 1|0 should not be in the same column, and neither should 3|2 and 4|2. We can resolve both by swapping 1|0 and 3|2 to get the following state:

We now have no column conflicts, but duplicates in rows 1 and 2, which can be resolved by swapping 2|1 and 1|0 to remove all remaining conflicts and solve the puzzle:

Generating games like these is simple to express in Prolog as a constraint logic program over integers:
:- use_module(library(clpfd)).
domicles([A-B,C-D,E-F,G-H,I-J,K-L,M-N,O-P]) :-
% All cells range from 0-6.
[A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P] ins 0..6,
% Grid rows should have distinct cells.
all_different([A,B,C,D]),
all_different([E,F,G,H]),
all_different([I,J,K,L]),
all_different([M,N,O,P]),
% Grid columns shuold have distinct cells.
all_different([A,E,I,M]),
all_different([B,F,J,N]),
all_different([C,G,K,O]),
all_different([D,H,L,P]),
% Flipping tiles is not allowed.
A#>=B,C#>=D,E#>=F,G#>=H,
I#>=J,K#>=L,M#>=N,O#>=P,
AB#=7*A+B,CD#=7*C+D,EF#=7*E+F,GH#=7*G+H,
IJ#=7*I+J,KL#=7*K+L,MN#=7*M+N,OP#=7*O+P,
% Tiles should not be re-used.
all_different([AB,CD,EF,GH,IJ,KL,MN,OP]),
label([A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P]).which can be run like this:
?- domicles(Solved),random_permutation(Solved,Shuffled).
Solved = [1-0,3-2,2-1,4-0,4-2,5-1,5-3,6-4],
Shuffled = [4-0,3-2,1-0,2-1,6-4,5-3,5-1,4-2]. Prolog will generate all possible puzzles on backtracking. I’ll leave randomising the order in which puzzles are generated and avoiding generating the same puzzle (but with different column/row order) as straightforward exercises for the reader.
GRADED DIFFICULTY
The 4x2 puzzles are easy, mostly because it is possible to resolve conflicts one at a time without having to think forward. However, to make the puzzle challenging, I just have to include more tiles. For example, here is a 4x3 layout:

The randomised version above can be unreasonably hard to solve because swapping tiles is likely to cause other conflicts, and you therefore have to think several moves ahead to avoid getting stuck.
The Prolog implementation of the 4x3 layouts is a direct extension of the simpler version, so I won’t dwell on it here. To make the difficulty configurable, I generate a solved puzzle and then perform N swaps at random (whilst making sure no swap accidentally solves the puzzle), so that the maximum distance to a solution is known:
swap(L,A-B,X) :-
nth1(A,L,V1),
nth1(B,L,V2),
replace(L,A,V2,X0),
replace(X0,B,V1,X).
replace(L,I,V,X) :-
nth1(I,L,_,R),
nth1(I,X,V,R).
shuffle(0,L,L) :-!.
shuffle(N0,A0,L) :-
N is N0-1,
findall(X-Y,(between(1,12,X),between(1,12,Y),Y>X),All0),
random_permutation(All0,All),
member(P,All),
swap(A0,P,A),
\+ puzzle(A),!,
shuffle(N,A,L).Here it is applied to the puzzle above so that it can be solved in at most 3 swaps:
?- domicles(Solved),shuffle(3,Solved,Shuffled).
Solved = [1-0,3-2,5-4,2-1,4-0,6-5,5-2,6-4,3-0,6-3,5-1,4-2]
Shuffled = [2-1,3-2,5-4,4-0,1-0,6-5,5-2,6-4,3-0,5-1,6-3,4-2]
If you’ve tried to do it you may have noted that the puzzle is still challenging but now solvable. I’ve observed that the difficulty of any Domicles puzzle seems related to the layout and the number of swaps used in the shuffle. The analysis below offers some insight into why that is the case.
A QUICK ANALYSIS
If I take as a standard that MxN layouts are rectangular with \(M\ge N\) (\(M\) are rows), then the possible number of Dominoes are either 1 or a multiple of 2. Double tiles cannot be used since they always violate the uniqueness rule, therefore the maximum number of tiles in a layout is 20 (e.g. 5x4).
The number of puzzle tile sets for a 4x2 layout, calculated by enumeration, is 6704. It is 2085 for a 4x3 layout. Meanwhile, the number of puzzles calculated by enumeration is 842,832 and 448,416 respectively. Of these, \(6704\times 4!\times 2! = 321792\) and \(2085\times 4!\times 3! = 403920\) are accounted for by variants of the intended solution. The total number of possible tile sets are \(C(21,8)=203490\) and \(C(21,12)=293930\) respectively. Many interesting things can be observed and deduced from these facts:
The difference between the layouts is just the addition of 1 row. I suspect that therefore the main effect is constraints on the columns, not the rows.
There are more than 3 times fewer puzzle tile sets for the 4x3 puzzle, and only \(2085/293930=0.007\) of possible tile sets constitute a 4x3 puzzle compared to \(6704/203490=0.033\) in the 4x2 case.
Corollary of 2, generally 4x2 puzzles cannot be “upgraded” to 4x3 puzzles by adding tiles since there are more of them. This has possible implications on whether puzzles can be solved by “divide and conquer” methods.
Tile sets at both sizes have more solutions (after variants are accounted for) than tile sets. In the 4x2 case, the number of puzzles imply \(841832/4!2!=17538.17\) tile sets but actually there are only 6704. Therefore, on average, there are \(17538.17/6704 = 2.62\) solutions per tile set. In the 4x3 case the puzzles imply \(448415/4!3! = 3114\) tile sets but there are actually 2085, hence on average, there are \(3114/2085 = 1.49\) solutions per tile set.
Any given 4x3 tile set will have \(12!\) possible arrangements of which \(1.49\times 4!3!=215\) will be solutions on average, compared to \(8!\) possible arrangements and \(2.62\times 4!2!=126\) solutions on average in the 4x2 case. That is, in the 4x3 layout there are \(4.5\times 10^{-7}\) solutions per arrangement, compared to \(3.1\times 10^{-3}\): a difference of 3 orders of magnitude.
From 5, if I were to define a distance matrix between arrangements of a particular tile set in terms of the number of tile swaps required to turn one arrangement into another, on average, the distances between arrangements in the 4x3 case would be bigger than that of the 4x2 case since – on average – there are more arrangements in between any given pair. I would expect these distances to be proportional to the number of arrangements, and therefore I expect the 4x3 layout to be exponentially more complicated than the 4x2 layout.
CONCLUSIONS
I’ve presented a configurable, fun and challenging logic puzzle which can be played with standard Dominoe tiles and implemented with a handful of Prolog. It required significantly more effort than this presentation may suggest to conceive the idea, but I learned a lot about how to construct combinatorial puzzles in the process. I’ve also provided a quick partial analysis with regards to the size and complexity of the puzzle, mostly because I needed to convince myself that the puzzles really do get harder as the number of tiles increase. Finally, I’ve left a few additional examples for you to try. Best enjoyed with some physical Dominoe tiles!
EXAMPLES
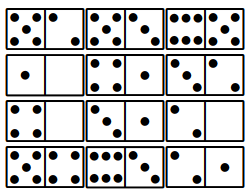
Rules: the tiles are arranged 4x3 resulting in a grid of 4x6 numbers. The aim of the game is to swap the tiles around such that every row and column in the 4x6 number grid has only unique values. The tiles cannot be flipped or rotated; just moved to different locations in the 4x6 layout.
Difficulty: 2-swaps

Difficulty: 3-swaps

Difficulty: 4-swaps
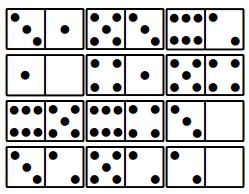
Difficulty: 5-swaps